Day 7

Advent of Code: Worked Solutions

Setup

Import libraries:

library(tidyverse)
library(unglue)
library(igraph)
library(tidygraph)
library(ggraph)

Read text input from file:

input <- read_lines("../input/day07.txt")

Convert text input into an igraph/tidygraph object. Bags that contain other bags are represented as a directed edge between two vertices, where the weight of the edge is the number of contained bags.

g <- input |> 
  unglue_data("{outer_color} bags contain {contains}.") |> 
  mutate(contains = str_split(contains, ", ")) |> 
  unnest_longer(contains) |> 
  unglue_unnest(
    contains, 
    "{num=\\d+} {inner_color} bag{=s?}", 
    convert = TRUE
  ) |> 
  select(outer_color, inner_color, weight = num) |> 
  drop_na() |> 
  graph_from_data_frame() |> 
  as_tbl_graph()

Plot the graph of the example input:

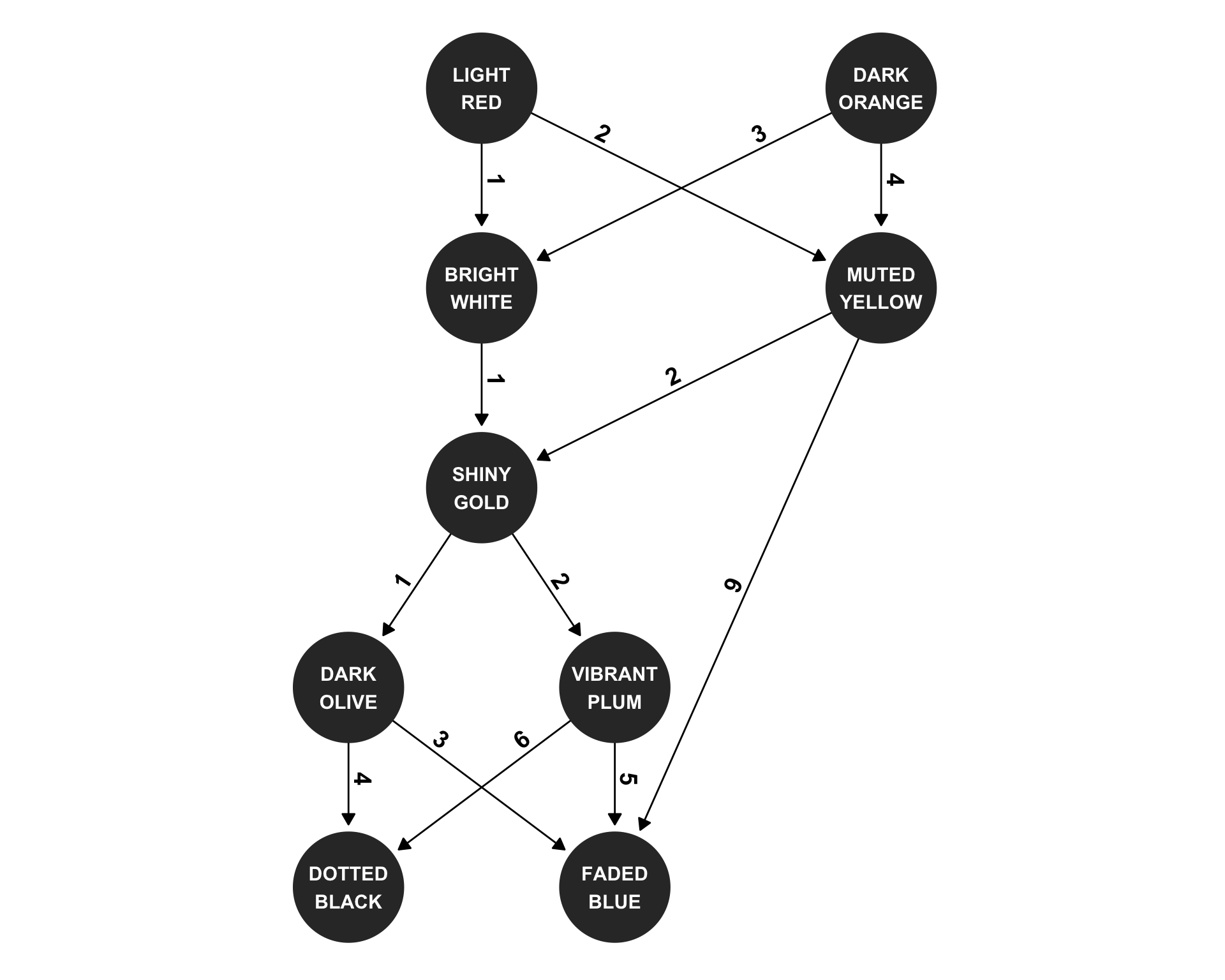
Part 1

Identify how many bag colors can eventually contain a “shiny gold” bag by counting the upstream ancestors of that vertex:

g |> 
  activate(nodes) |> 
  mutate(n_ancestors = local_size(order = graph_order(), mode = "in") - 1) |> 
  as_tibble() |>
  deframe() |> 
  pluck("shiny gold")

Part 2

First, get the list of all vertices downstream from “shiny gold”:

src <- as.numeric(V(g)["shiny gold"])

downstream <- g |> 
  activate(nodes) |>
  mutate(neighbors = local_members(order = Inf, mindist = 1, mode = "out")) |>
  as_tibble() |> 
  deframe() |> 
  pluck("shiny gold")

For each vertex downstream from “shiny gold”, get the list of ALL paths from the “shiny gold” vertex to the downstream vertex, and convert to an order list of the weights:

path_weights <- map(downstream, ~ all_simple_paths(g, src, to = .x)) |> 
  list_flatten() |> 
  map(\(path) {
    map_int(2:length(path), \(id) {
      get_edge_ids(g, path[c(id - 1, id)])
    })
  }) |> 
  map(\(edge_set) E(g)$weight[edge_set]) 

Compute the product of the weights in each path, then sum up the result from all paths. For example: if bag A contains 2 of bag B, and bag B contains 3 of bag C, then the final count of bag B is 2 and bag C is 6 (= 2 * 3).

path_weights |> 
  map_int(prod) |> 
  sum()