Day 10

Advent of Code: Worked Solutions

Setup

Import libraries:

library(tidyverse)
library(igraph)
library(tidygraph)
library(ggraph)

Disable scientific formatting when displaying large numbers:

options(scipen = 999)

Read text input from file into a numeric vector:

input <- scan("../input/day10.txt")

Part 1

Determine the differences between each jolt value ranked in order so that all are used, manually including the “0” starting point and the output rating of max(input) + 3. Compute the total number of 1, 2, and 3-jolt differences:

dist <- c(0, input, max(input) + 3) |> 
  sort() |> 
  diff() |> 
  sort() |> 
  rle()

Multiply the count of 1-jolt differences by the count of 3-jolt differences:

dist$lengths |> 
  keep(dist$values %in% c(1, 3)) |> 
  prod()

Part 2

Convert the list of adapters (including the “0” input and final output) into a graph.

g <- expand_grid(
  v1 = c(0, sort(input), max(input) + 3),
  v2 = c(0, sort(input), max(input) + 3)
) |> 
  filter(between(v2 - v1, 1, 3)) |> 
  graph_from_data_frame()

Get the list of all separators from the grap (vertices which disconnect the graph if removed):

sep <- g |> 
  as_undirected() |> 
  min_separators() |> 
  map_chr(names)

The graph of the “small example” in the problem description is shown below, with ends colored green, separators black, and non-separators (nodes which can be individually removed without disconnecting the graph) red:

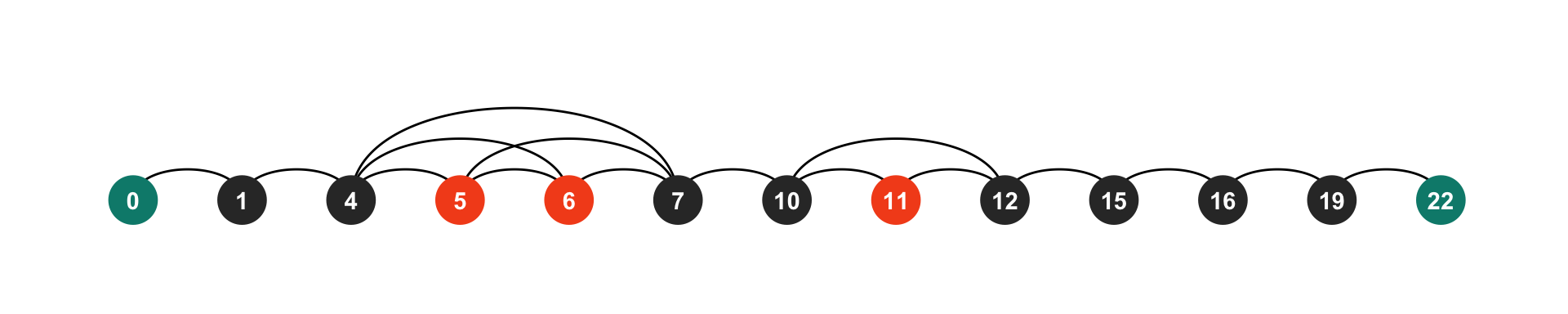
For each pair of separators in order, determine the number of possible paths between them. To get the final total count of paths, multiply the result of all pairs together:

sep <- sort(as.numeric(sep))

map2(c(0, sep), c(sep, max(input) + 3), \(v1, v2) {
  g |> 
    all_simple_paths(
      as.character(v1), 
      as.character(v2), 
      mode = "out",
      cutoff = v2 - v1
    )
}) |> 
  map_int(length) |> 
  prod()