Day 23

Advent of Code: Worked Solutions

Setup

# Libraries
library(tidyverse)
library(igraph)

# Read input from file
input <- read_lines("../input/day23.txt", skip_empty_rows = FALSE)

Part 1

Convert text input to a directed graph:

# Convert to a dataframe with IDs and coordinates per cell
df <- input |> 
  str_split("") |> 
  enframe(name = "row") |> 
  unnest_longer(value, indices_to = "col") |> 
  mutate(id = row_number()) |> 
  filter(value != '#') |> 
  relocate(id, value, row, col)

# Compute the list of directed edges between cells
edges <- df |> 
  mutate(
    row_n = row - 1,
    row_s = row + 1,
    col_w = col - 1,
    col_e = col + 1
  ) |> 
  left_join(df, join_by(x$row_n == y$row, col), suffix = c("", "_n")) |> 
  left_join(df, join_by(x$row_s == y$row, col), suffix = c("", "_s")) |> 
  left_join(df, join_by(x$col_w == y$col, row), suffix = c("", "_w")) |> 
  left_join(df, join_by(x$col_e == y$col, row), suffix = c("", "_e")) |> 
  select(-starts_with(c("row", "col", "value_"))) |> 
  pivot_longer(
    starts_with("id_"),
    names_to = "dir",
    values_to = "neighbor",
    names_prefix = "id_"
  ) |> 
  
  # For slope tiles, remove any non-downhill neighbors
  filter(
    (value == "." & !is.na(neighbor)) |
      (value == "^" & dir == "n") | 
      (value == "v" & dir == "s") |
      (value == "<" & dir == "w") | 
      (value == ">" & dir == "e") 
  ) |> 
  pmap(\(id, neighbor, ...) c(id, neighbor)) |> 
  unlist()

# Convert to a graph
g <- make_graph(edges)

Find the longest possible path from the start point to the end point:

source <- min(df$id)
target <- max(df$id)

max_hike <- function(g, from = source, to = target) {
  all_simple_paths(g, from, to) |> 
    map_dbl(~ length(.x) - 1) |> 
    sort(decreasing = TRUE) |> 
    max()
}

max_hike(g)

[1] 2074

Part 2

Convert to an undirected graph to remove the slope constraint:

g <- as_undirected(g)
V(g)$name <- V(g)

The graph is too large to simply run the hike length function again – an overflow results.

Instead, we notice that the input maze consists of relatively few intersections. Most of the maze input is simple corridors with no path decisions. We can reduce the graph complexity/size by trimming away our non-choice verftices and converting the length of those paths to an edge weight.

v_zero_edges   <- names(which(degree(g) == 0))
v_two_edges    <- names(which(degree(g) == 2))
v_nontwo_edges <- names(which(degree(g) != 2))

# Extract all corridor vertices
g_corridors <- delete_vertices(g, v_nontwo_edges)
corridors <- components(g_corridors)

# Determine which edges to add to replace the corridors and their weight
new_weights <- corridors$csize + 1
new_edges <- corridors$membership |> 
  keep_at(names(which(degree(g_corridors) == 1))) |> 
  enframe(name = "vtx", value = "group") |> 
  mutate(vtx = map_chr(vtx, ~ setdiff(names(neighbors(g, .x)), v_two_edges))) |> 
  summarize(edge = list(vtx), .by = group) |> 
  arrange(group) |> 
  pull(edge)

# Create a new graph without the corridor vertices, then add its new edges
g_new <- reduce2(
  .x = new_edges,
  .y = new_weights,
  .f = \(g, e, w) add_edges(g, e, weight = w),
  .init = delete_vertices(g, c(v_zero_edges, v_two_edges))
)

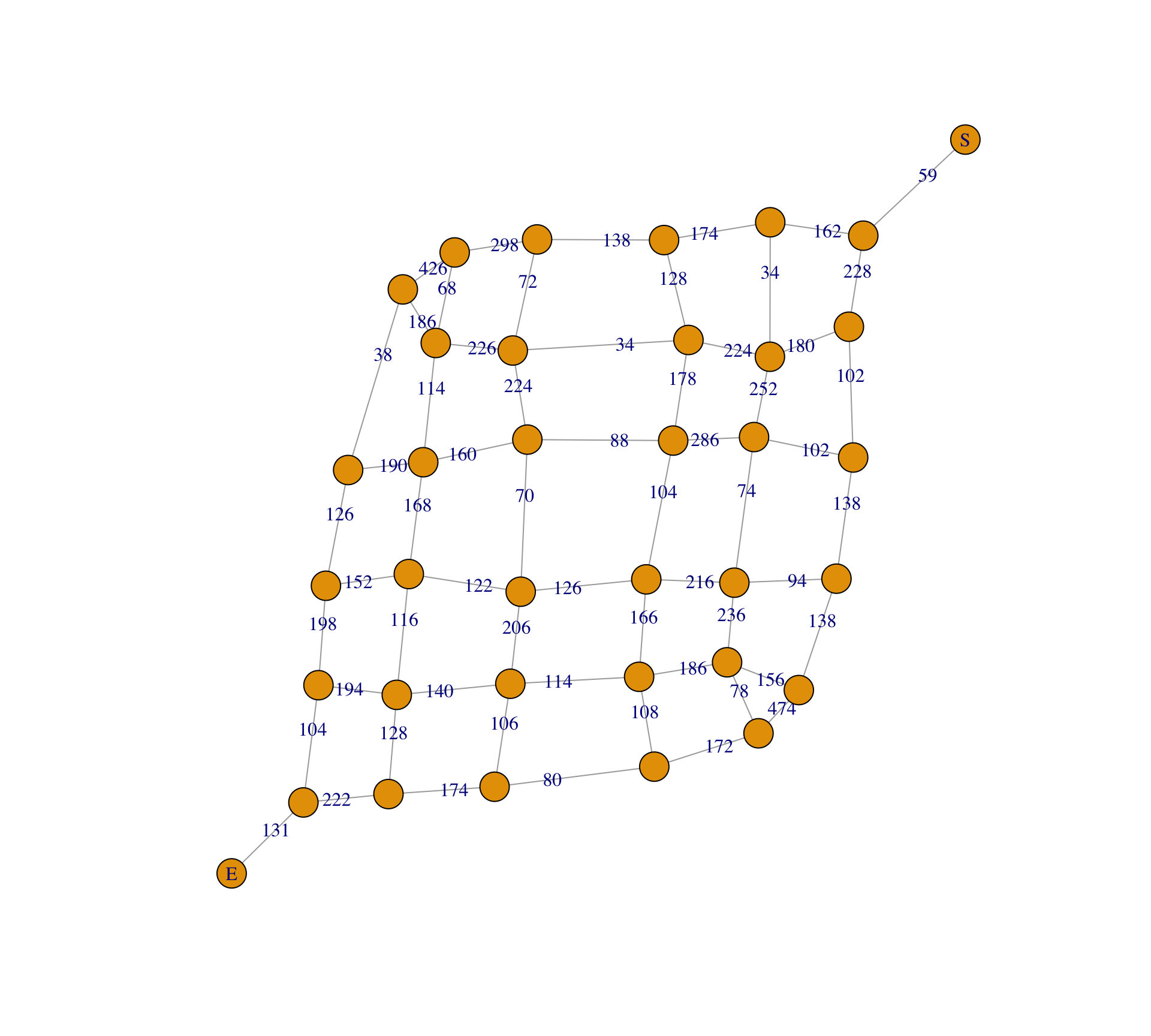
View a plot of the resulting simplified graph:

vtx_labels <- g_new |> 
  V() |> 
  names() |> 
  case_match(
    as.character(source) ~ "S", 
    as.character(target) ~ "E", 
    .default = ""
  )

plot(
  g_new, 
  vertex.size = 8,
  vertex.label = vtx_labels, 
  edge.label = E(g_new)$weight
)

Compute all paths from the start to the end using our smaller graph:

all_paths <- g_new |> 
  all_simple_paths(as.character(source), as.character(target))

Using the edge weights of our graph, compute the total length of each path and select the longest:

all_paths |> 
  map(
    ~ .x |> 
      as_ids() |> 
      rep(each = 2) |> 
      head(-1) |> 
      tail(-1) |> 
      get_edge_ids(graph = g_new)
  ) |> 
  map(~ E(g_new)$weight[.x]) |> 
  map_dbl(sum) |> 
  max()

[1] 6494